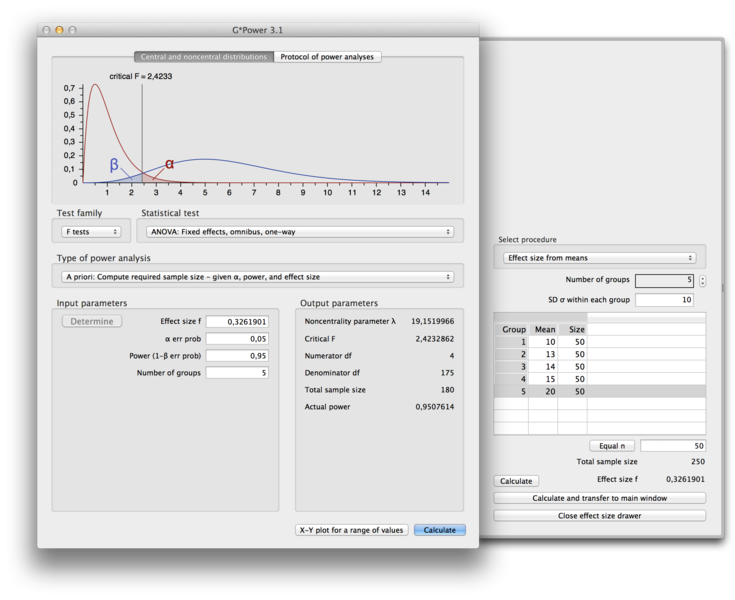
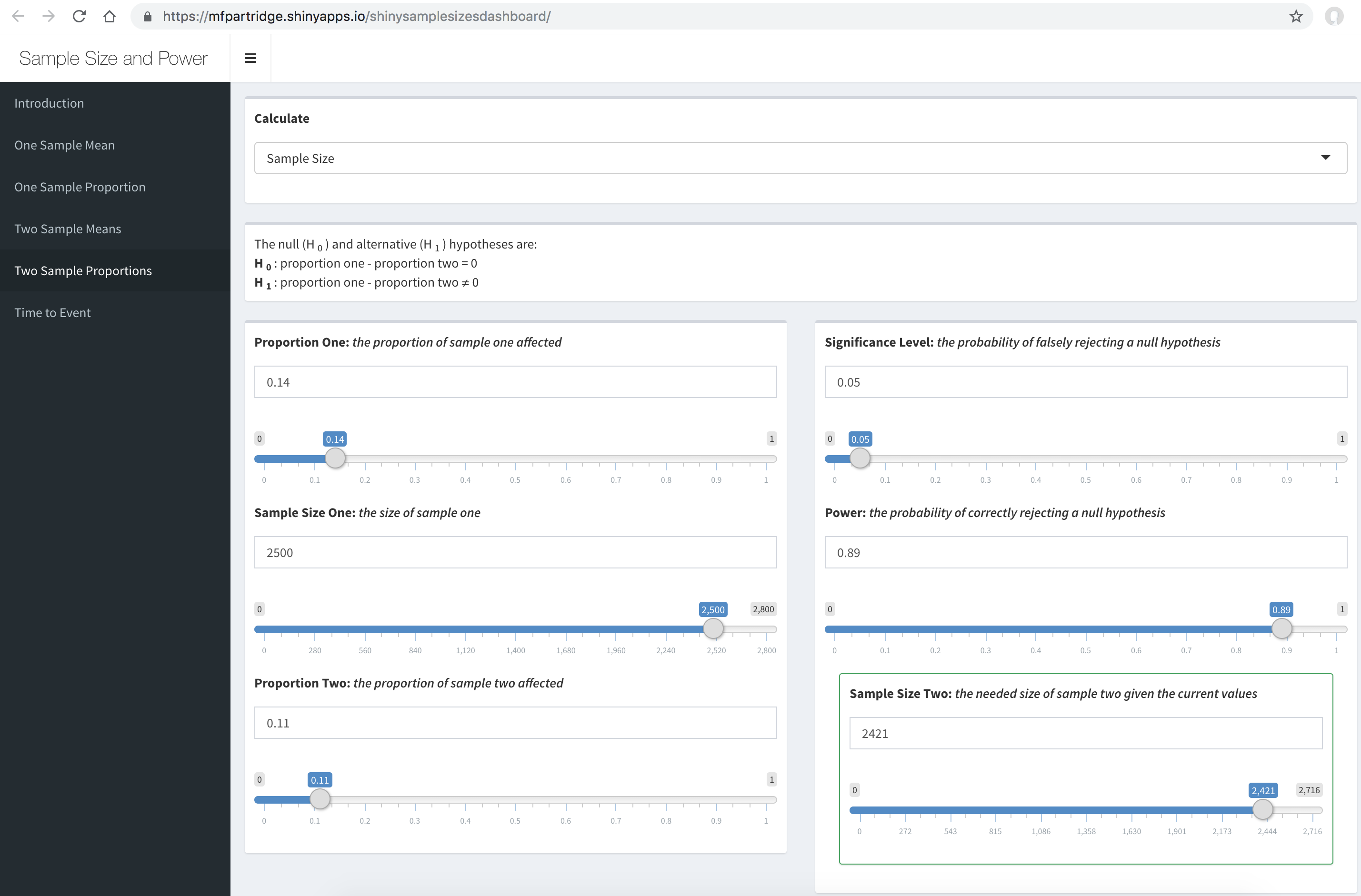
Is n=3 enough? How to approach sample size and power calculations

# Is n=3 enough? How to approach sample size and power calculations
### Jessica Minnier, PhD Knight Cancer Institute Biostatistics Shared Resource Oregon Health & Science University
### <a href="https://www.abstractsonline.com/pp8/#!/6812/session/153">AACR</a>, March 30, 2019 <a href="https://bit.ly/aacr-power">bit.ly/aacr-power</a> <a href="https://twitter.com/datapointier">datapointier</a>

---

---

# Goals of sample size and power calculations

- Design a study that will have enough information about underlying population to reject a hypothesis with high confidence.
- Calculate the number of sampling units (e.g. people, animals) you need to estimate statistics with a certain level of precision.

---

# Design your study

---

# Step 1: State your research hypothesis

- Define your:
    + Population
    + Outcome variables/measurements
    + Predictor variables (i.e. treatment, age, genetic mutation)
- Be specific!
- Example: Among *women* (population you sample from), the *BRCA1* mutation
(predictor) is associated with an increased risk of developing *breast cancer* (outcome).
- **Question**: How many women do we need to sample/study to determine that BRCA1 is associated with breast cancer?

## Your hypothesis and design inform your analysis method.

---

# Step 2: Choose your analysis and test(s)

- You can't calculate sample size without knowing which test and model you will use.
- How will you measure your outcome? Continuous? Categorical? Binary (yes/no)?
    + choose outcomes with high sensitivity and low measurement error
- How many groups/experimental conditions/predictors?
    + the more you have the more samples you will need
- What test? t-test? Linear regression? Random effects model? Chi-square test?

## Calculate sample size based on analysis method you will use.

---

# Calculate power and sample size

---

# Need to know (/tell your statistician!):

- Overall design (outcome, endpoint, hypothesis)
- Size/magnitude of effect of interest
    + What do you *hope* to detect
- Variability of measurements
    + Precision of your measurement, biological variability within population
- Level of type I error (false positive rate, significance level, `\(\alpha\)`)
- Level of power (true positive rate)
- Other design details (number of groups, clustering, repeated measures)

---

# Components of Sample Size

Need to know 3 of the 4 to determine the 4th:

Do We Know? | Measure | Definition
---|---|---
?? | Effect Size | Magnitude of difference or association; i.e. (difference in means)/(population standard deviation) = `\(\frac{\mu_1 - \mu_0}{\sigma}\)` = `\(\frac{\delta}{\sigma}\)`
?? | Sample Size | N
0.05, 0.01 | Type I Error / Significance level | `\(\alpha\)` = probability of rejecting null hypothesis when it is true
0.9, 0.8 | Power | 1 - `\(\beta\)` = 1 - Type II error = probability of rejecting null hypothesis when it is false

---

# What is **effect size**?

- Summarizes the outcome of interest
- Magnitude of difference or association
- Specification depends on study design and statistical model/test

## Examples:

- Difference in treatment and control mean outcomes, relative to variance (standard deviation)
- Correlation coefficient of two biomarkers
- Risk ratio of breast cancer comparing BRCA carriers to non-carriers
- Magnitude of regression coefficient

---

# Effect size must be

- **pre-specified**
- based on what is meaningful biologically or clinically (not statistical significance)
- based on pilot data or literature review if available

---

# Simple example: T-test

Outcome = Continuous measurement, normal distribution

Predictor = Treatment yes/no (treatment vs control group)

Test: two sample T-test, equal variance

Effect Size: difference in means divided by standard deviation of population `\(\frac{\mu_{trt} - \mu_{ctrl}}{\sigma}\)`

Null Hypothesis: Difference in means = 0

Alternative Hypothesis: Difference in means `\(\neq\)` 0

**"Given a desired effect size, what sample size gives us enough information to reject the null hypothesis with power 90%, type I error 5%?"**

---

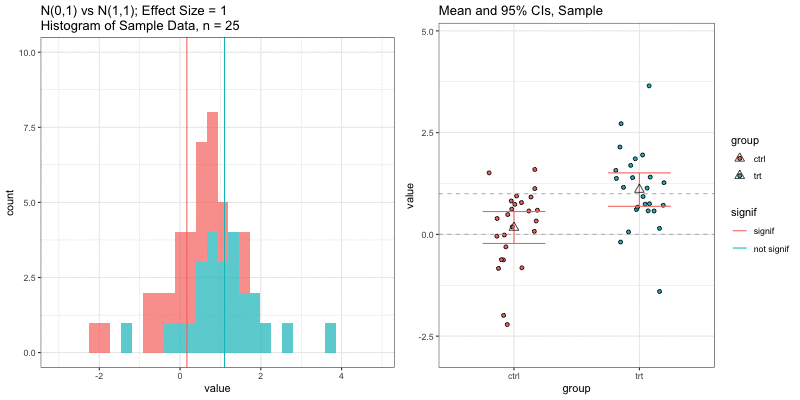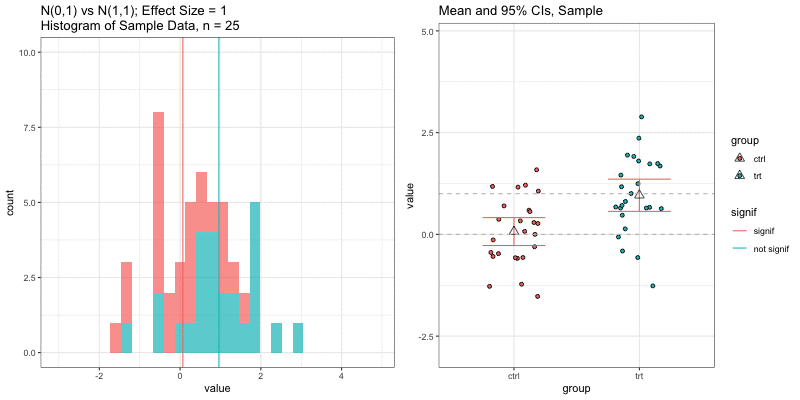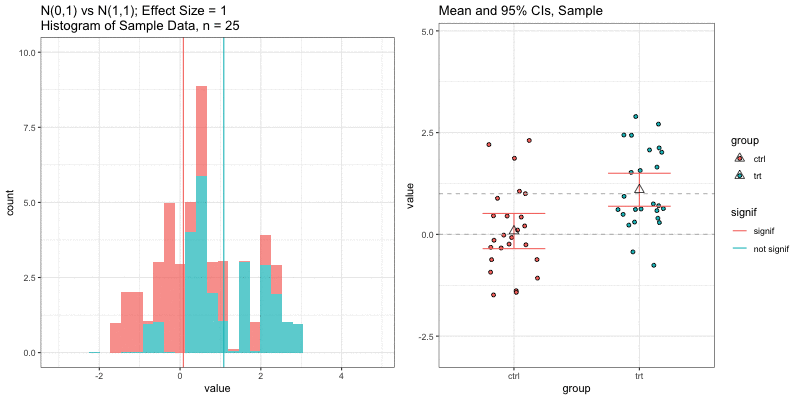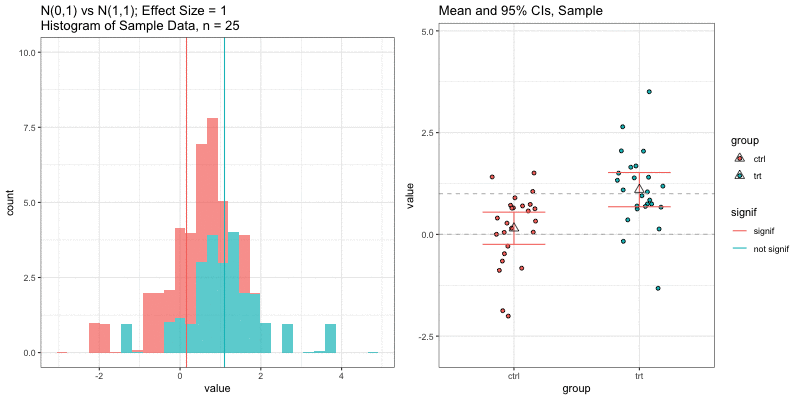
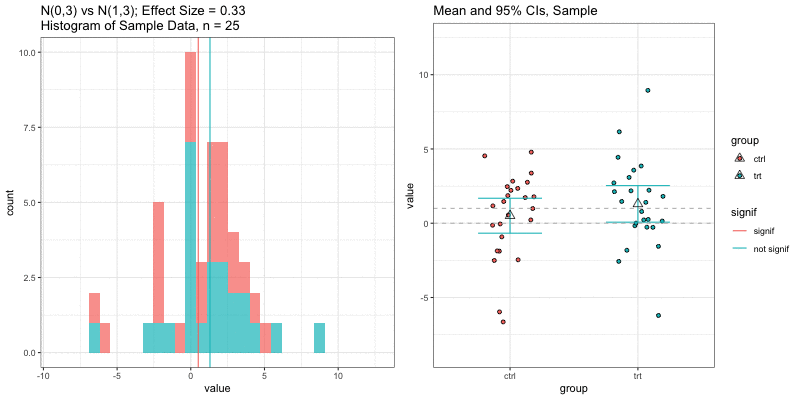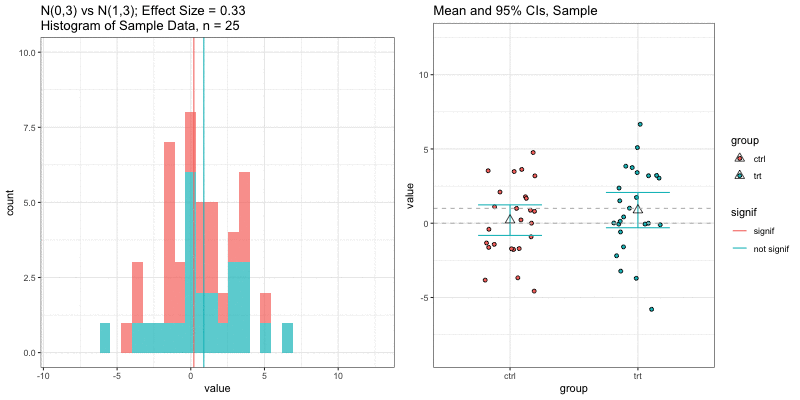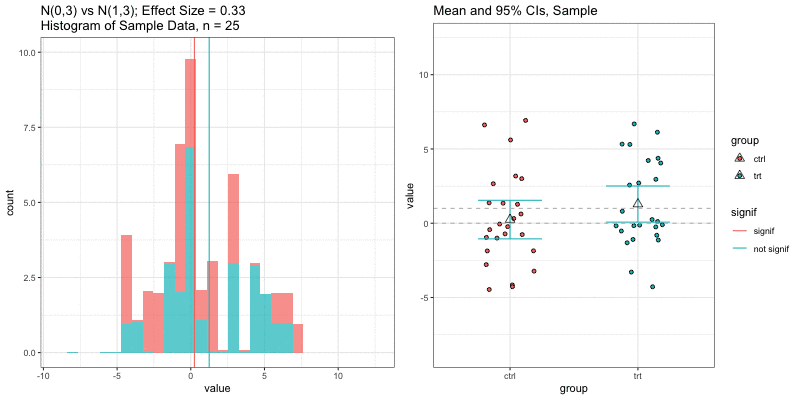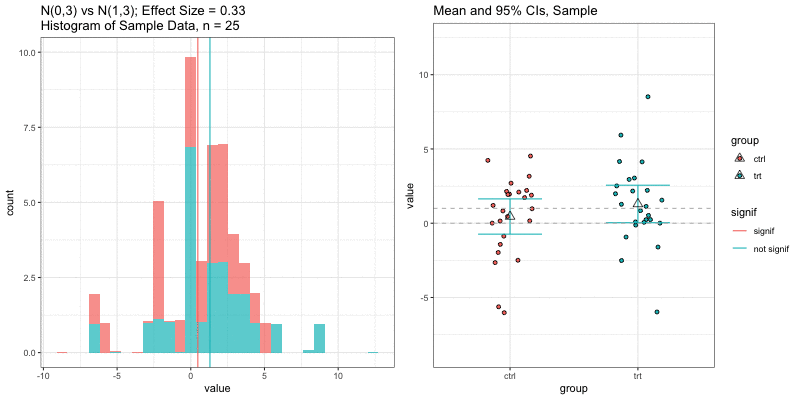
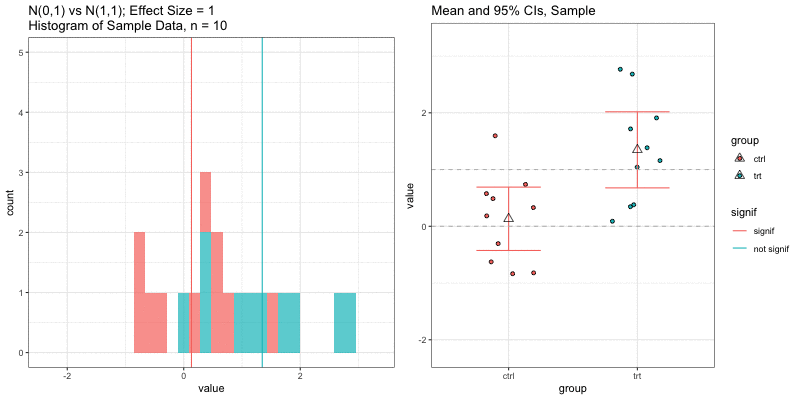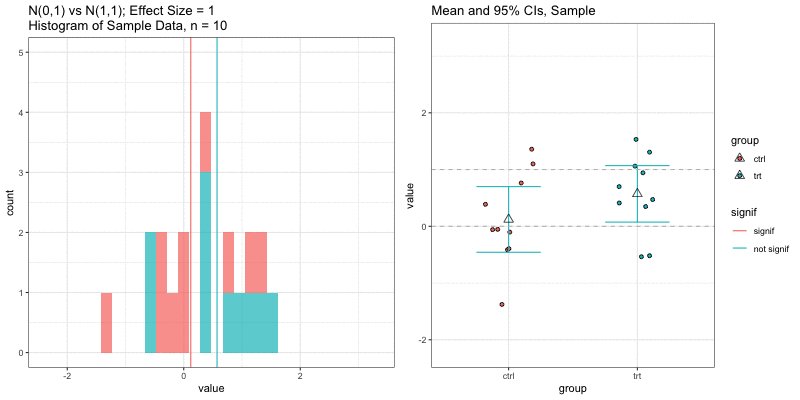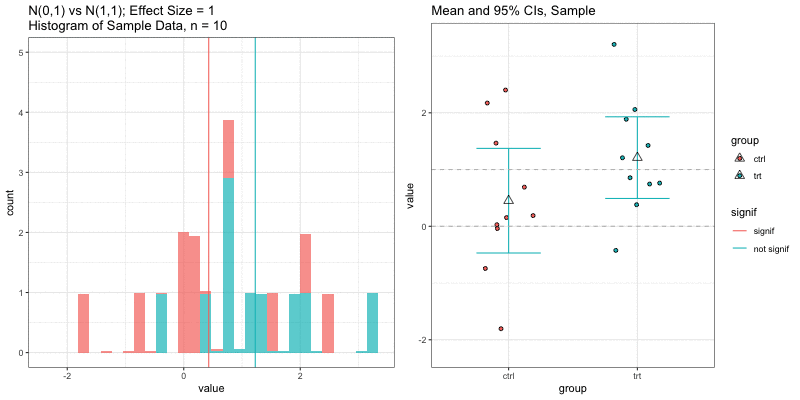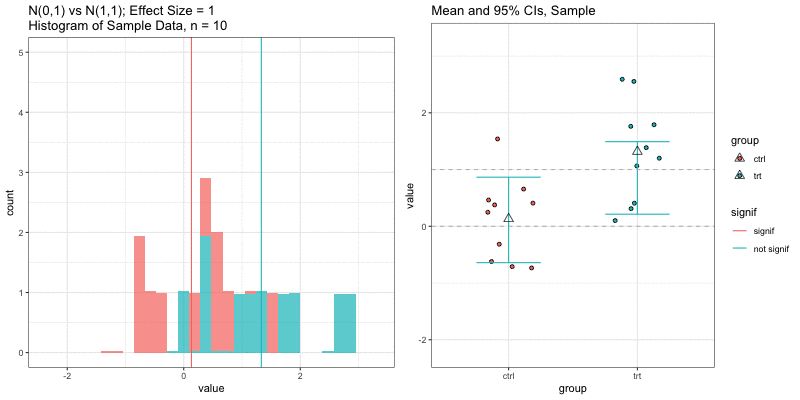
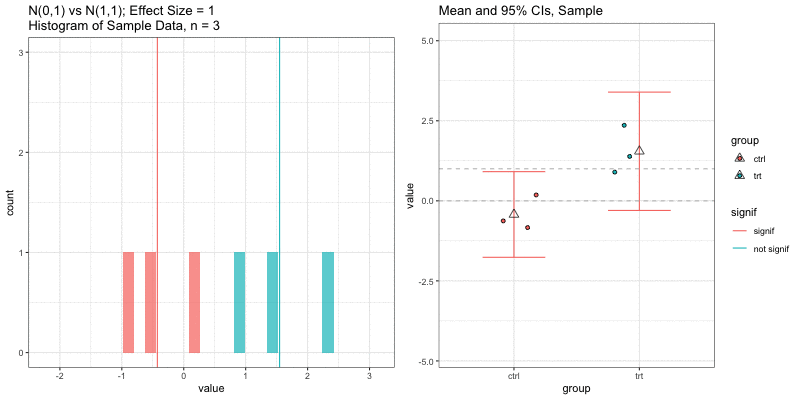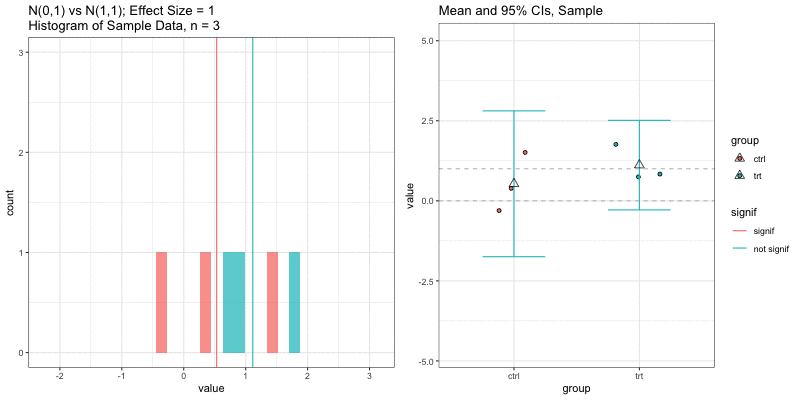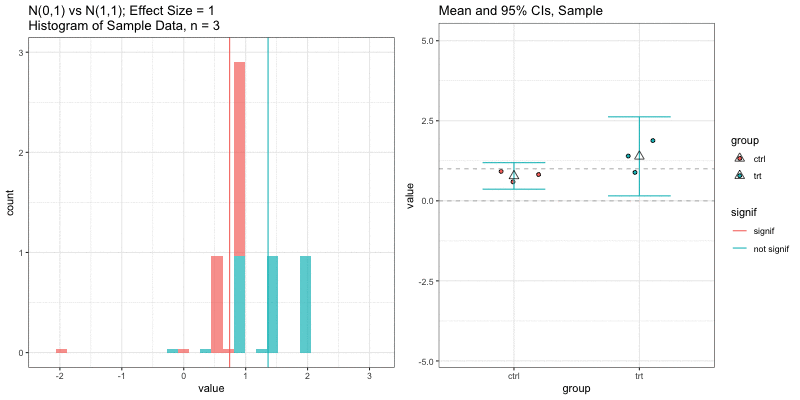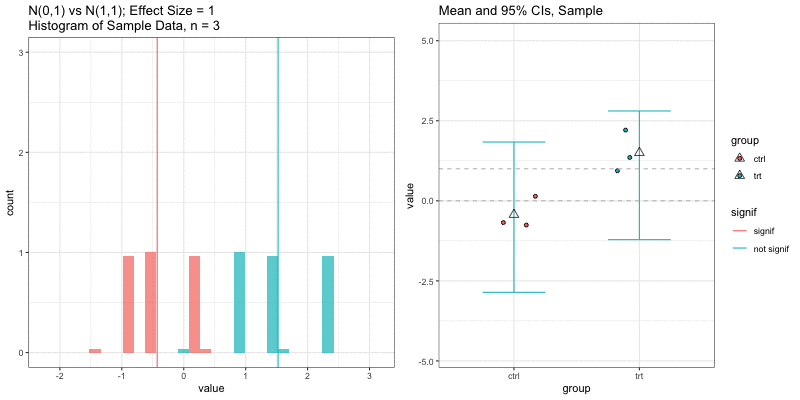
# Simulations: underlying data distributions

<img src="2019_03_AACR_Minnier_files/figure-html/normal_true-1.png" style="display: block; margin: auto;" />
---

# n=25, effect size = 1

Power = 0.93 
(Significance based on two sample t-test for difference in means)

---

# n=25, effect size = 0.33

Increase standard deviation from 1 to 3, divides effect size by 3
 Power = 0.21

---

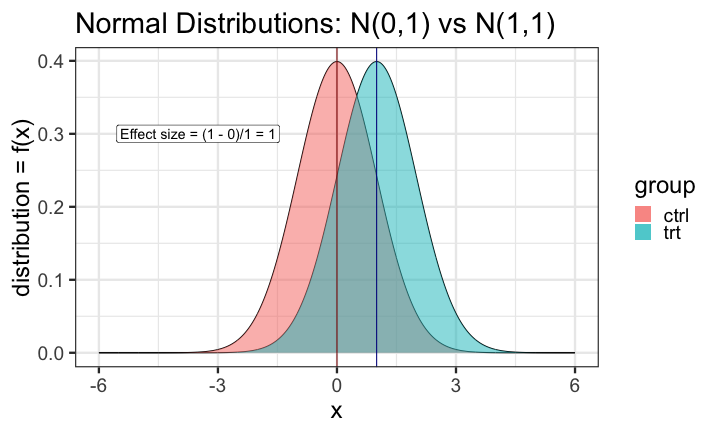
To detect an effect size of 0.33 with power = 0.9 and type I error = 0.05, what sample size would we need? n=194 in each group!

```r
power.t.test(delta = 0.33, sd = 1, sig.level = 0.05, power = 0.9)
```

```

Two-sample t test power calculation

n = 193.9392
          delta = 0.33
             sd = 1
      sig.level = 0.05
          power = 0.9
    alternative = two.sided

NOTE: n is number in *each* group
```

---

# n=10, effect size = 1

Decrease sample size 
Power = 0.56

---

# n=3, effect size = 1

Decrease sample size even more Power = 0.16

---

# n = 3, power = 0.9, effect size = ?

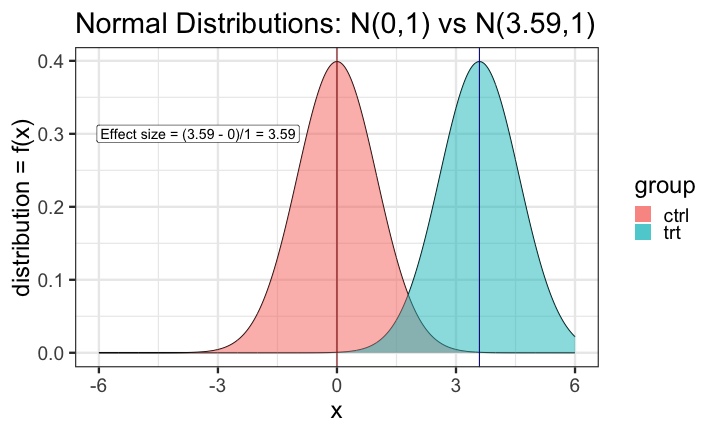
In the `R` output below, the effect size is delta/sd = 3.59/1 = 3.59.

```r
power.t.test(n=3, sd=1, sig.level=0.05, power=0.9)
```

```

Two-sample t test power calculation

n = 3
          delta = 3.589209
             sd = 1
      sig.level = 0.05
          power = 0.9
    alternative = two.sided

NOTE: n is number in *each* group
```

---

# Underlying data distributions

---

# Other reasons to calculate sample size

## Precision of statistics

- Sample sizes can also be calculated for a specific maximum width in confidence interval around an estimate
- i.e. we will estimate the proportion with a 95% confidence interval of width 0.1 such as [0.2, 0.3]

## Prediction models

- Large sample sizes are needed for complex prediction models.
- Stability of prediction model accuracy measures depends on sample size.

---

# Important to remember:

## Sample size estimates are ESTIMATES.

- based on assumptions that could be incorrect
- based on pilot data that could be a poor sample or too small
- the more you don't know, the more conservative you should be (inflate your `\(n\)`)
- good to provide multiple estimates for a variety of scenarios/effects

---

# Free online software

---

# [G*power](http://www.gpower.hhu.de/)

(examples of how to use it: http://www.ats.ucla.edu/stat/gpower/)

![](img/gpower.png)

---

# [Shiny Dashboard for Sample Size and Power Calculations](https://mfpartridge.shinyapps.io/shinysamplesizesdashboard/)

![](img/software1.png)

---

# Others

- [TrialDesign.org](http://www.trialdesign.org/index.html)
- [GLIMMPSE](https://glimmpse.samplesizeshop.org/#/)
- [CRAB Stat tools](https://stattools.crab.org/)
- [The Shiny CRT Calculator: Power and Sample size for Cluster Randomised Trials](https://clusterrcts.shinyapps.io/rshinyapp/)
- [Cal Poly Stats Dept Apps](https://statistics.calpoly.edu/shiny)
- Statistical software such as R, SAS, STATA

---

# Take home message:

## Do your research before you do your research!

---

# Thank you!

Contact me: minnier-[at]-ohsu.edu, [datapointier](https://twitter.com/datapointier), [jminnier](https://github.com/jminnier/)

Slides available: [bit.ly/aacr-power](https://bit.ly/aacr-power)

Slide code available at: [github.com/jminnier/talks-etc](https://github.com/jminnier/talks_etc)

# References

- Some of this talk adapted from: [David Yanez's Sample Size](https://www.ohsu.edu/xd/research/centers-institutes/octri/education-training/upload/PowerAndSampleSize.pdf) talk at [OCTRI Research Forum (OHSU)](https://www.ohsu.edu/xd/research/centers-institutes/octri/education-training/octri-research-forum.cfm)
- [Statistical Rules of Thumb, Chapter 2](http://www.vanbelle.org/)